VBA Atn 関数正接(tan)の値から角度を求めます

2026年2月12日

Excel VBAの「Atn 関数」について解説します。

Atn 関数とは

Excel VBA の Atn 関数は、正接(tan)の値から角度を求めるための関数です。角度計算・方向計算・傾き判定などに使われます。

Atn 関数の構文や実際の使い方について具体的に解説していきたいと思います。

Atn 関数(Visual Basic for Applications リファレンス)

構文（引数と戻り値）

Excel VBAの関数を使いこなすには、関数の構文を正しく理解しておくことが重要です。

構文

Atn(number)

引数

指定項目	説明
number	【必須】タンジェントを表す任意の有効な Double型の数値(式)

※ tan(タンジェント)とは、直角三角形の高さを底辺で割った値です。（高さ÷底辺）

戻り値

角度（ラジアン）を返します。【度数法の度°ではなくラジアンである点に注意！】

戻り値の範囲は、-π/2 ～ +π/2 (-90°～ +90°) です。

単位「ラジアン」とは

ラジアンとは数学の角度を表す単位で
「円（扇形）の孤の長さ(L)÷円の半径(r)」によって求められる値のことです。

度°をラジアンに変換するには次のように計算します。

度°= ラジアン × 180 / π

VBA では、「度°＝ラジアン * 180 / WorksheetFunction.Pi()」です。

[注意] VBA の Atn() 関数は、Excel の ATAN() 関数と同等です。
奇妙なことに、WorksheetFunctions.ATAN() は存在しません (他の Excel 数式関数と同様)。

Tan(90度) 解説（使用例）

ここからは、サンプルを使って使用例や注意点などについて解説します。

Atn 関数の基本的な使い方

Tan値から角度を求める

Tan値 = 1 から角度°を求める例です。

'■Atn関数サンプル１（tan=1の角度は）
Sub Atn_Sample_01()
  Dim rad As Double   'ラジアン=Radians
  Dim deg As Double   '度=degrees
  
  rad = Atn(1)  'tan値 = 1
  deg = rad * 180 / WorksheetFunction.Pi()
  
  MsgBox "tan値 = 1 の角度は " & deg & "° です"
End Sub

実行結果がこちらです。

タンジェント 1 は 45度です。

セルの値を使って角度を計算する

次の例は、セルの値(Tan値)を取得して計算結果をセルに書き込む方法です。
Tan関数のサンプルで使用したデータ(B列)を使って、変換後の結果をC列に書き込みます。

'■Atn関数サンプル２（セル値を取得して計算する）
Sub Atn_Sample_02()
  Dim Deg As Double   '度=degrees
  Dim rad As Double   'ラジアン=Radians
  Dim i As Long

  For i = 2 To 14
    rad = Atn(Cells(i, 3))  'C列Tan値を取得
    Deg = rad * 180 / WorksheetFunction.Pi() '度に変換
    Cells(i, 4).Value = rad 'D列にAtn値を書き込む
    Cells(i, 5).Value = Deg 'E列に角度を書き込む
  Next i
End Sub

Tan関数のサンプルデータ(B列)は、拡散地補正前の生データ値を使っています。
実行結果のワークシート画像がこちらです。

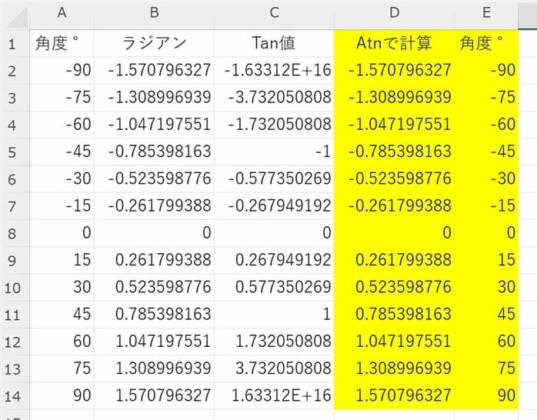
背景が黄色のセルが書き込まれた数値です。

Tan値(C列)を挟んで、Atn値(D列)＝ラジアン(B列)、角度°(E列)＝角度°(A列) となっています。

Atn関数が Tan関数と逆の動きをする関数であることがよくわかりますね。

傾き(勾配)から角度を求める例

Atn関数が使われる例の一つ、屋根や道路の勾配計算などによく使われます。

'■Atn関数サンプル３（傾き(勾配)から角度を求める）
Sub Atn_Sample_03()
  Dim slope As Double '勾配(傾き)
  Dim Deg As Double   '角度=degrees
  
  slope = 0.25   '25%の勾配(100mで25m登る)=Tan値
  Deg = Atn(slope) * 180 / WorksheetFunction.Pi()
  
  MsgBox Deg & "°" '角度を表示する
End Sub

実行結果

約14°ですね。

まとめ

おわりに

VBA の Atn 関数は、Tan(正接)の値から角度(ラジアン)を求めるための関数です。
「Tanの逆関数」という位置づけです。

Atn 関数の戻り値はラジアンです
度数法の角度(°) を得るためには「ラジアン × 180 / π」での変換が必須です
Atn 関数は Tan(傾き)の角度を表すラジアンを返しています
Ata 関数の戻り値の範囲は -π/2 ～ +π/2 (-90°～ +90°)です
座標角度には象限処理を考慮する（象限とは次のとおり）
- 原点から右上に伸びる → 第1象限（0°～90°）
- 左上に伸びる → 第2象限（90°～180°）
- 左下に伸びる → 第3象限（180°～270°）
- 右下に伸びる → 第4象限（270°～360°）
Atn関数単体では「傾き」しか分からないため、 方向（象限）まで求めたい場合はXとYの両方の符号(±)をみる必要があります。